
Various schemes are possible for the semifinals and finals of a sport with three teams per game, such as Zone. Here are several. Click for larger images.
Usually the top team going in to each game has first choice of colour, the second team has second choice, and the third team gets what they get.
Ascension, Skip Ascension, Format D, Two Track, Double game before finals, other.This is the old-style straight Ascension. Note my amusing habit of numbering games backwards.
Ascension requires one game per team (including the three game grand finals series). The average team will play three games.

Strategy: Don't come third.
Advanced Strategy: Choose which of the two teams you are playing now that you would prefer to play again in the next game. Play to make the remaining team come third.
Pros:
Cons:
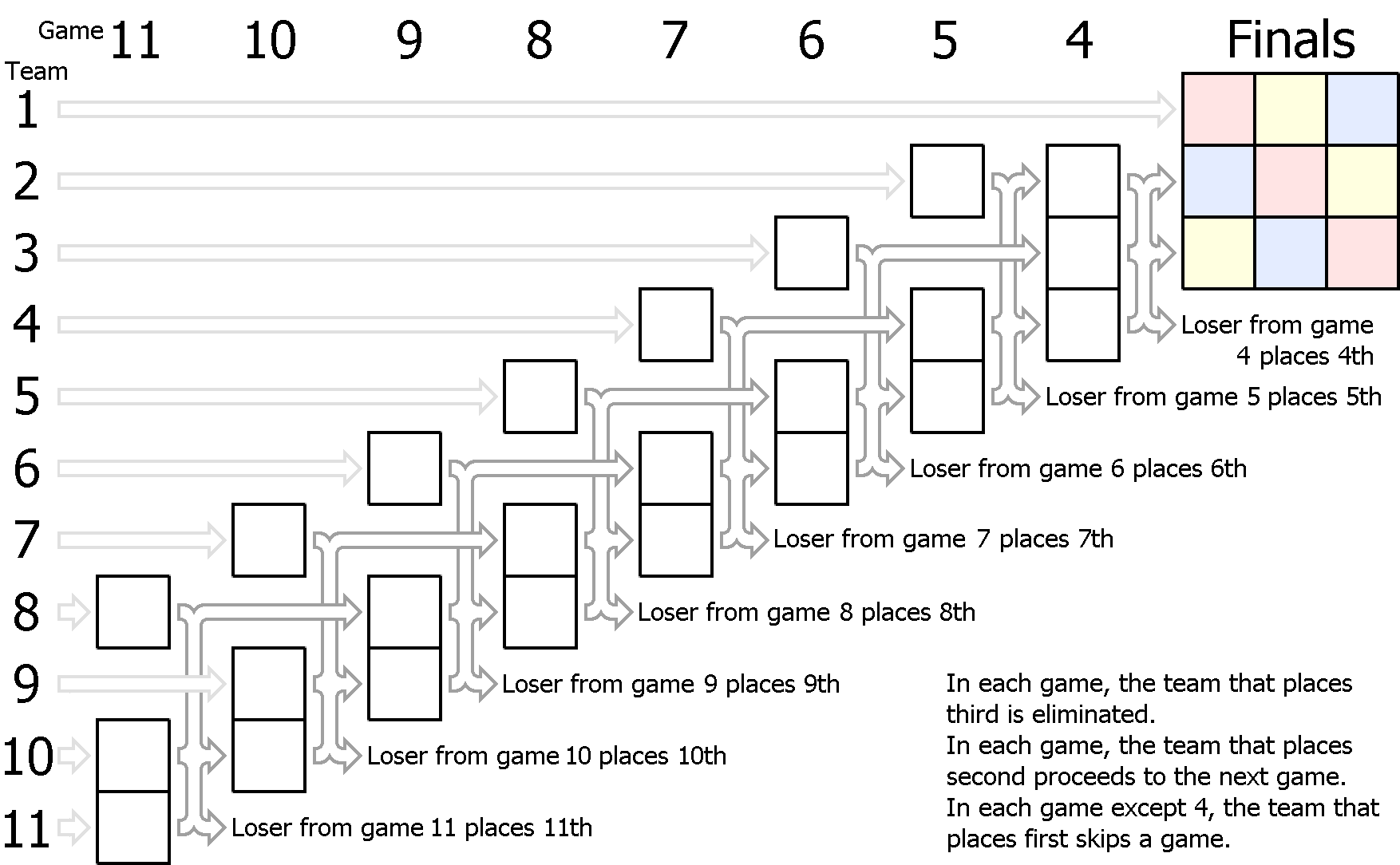
Below is the Skip Ascension as used in 2005 and 2006. In this version, the #1 team gets a bye straight through to the grand finals. Additionally, the n-2th team (in this case, the 9th team) gets a bye through the first game.
Skip Ascension also requires one game per team (including the three game grand finals series), and the average team will play three games.
Below is a slightly different Skip Ascension: at the top, team 1 does not get a bye: they must play one game to get to finals. This means that team 2 plays only one game to get to finals instead of two. Additionally, the n-2th team does not get a bye: they are in the very first game. (Of course, you could draw two other similar grids, with a bye for team 1 but not for team n-2, or vice versa.)
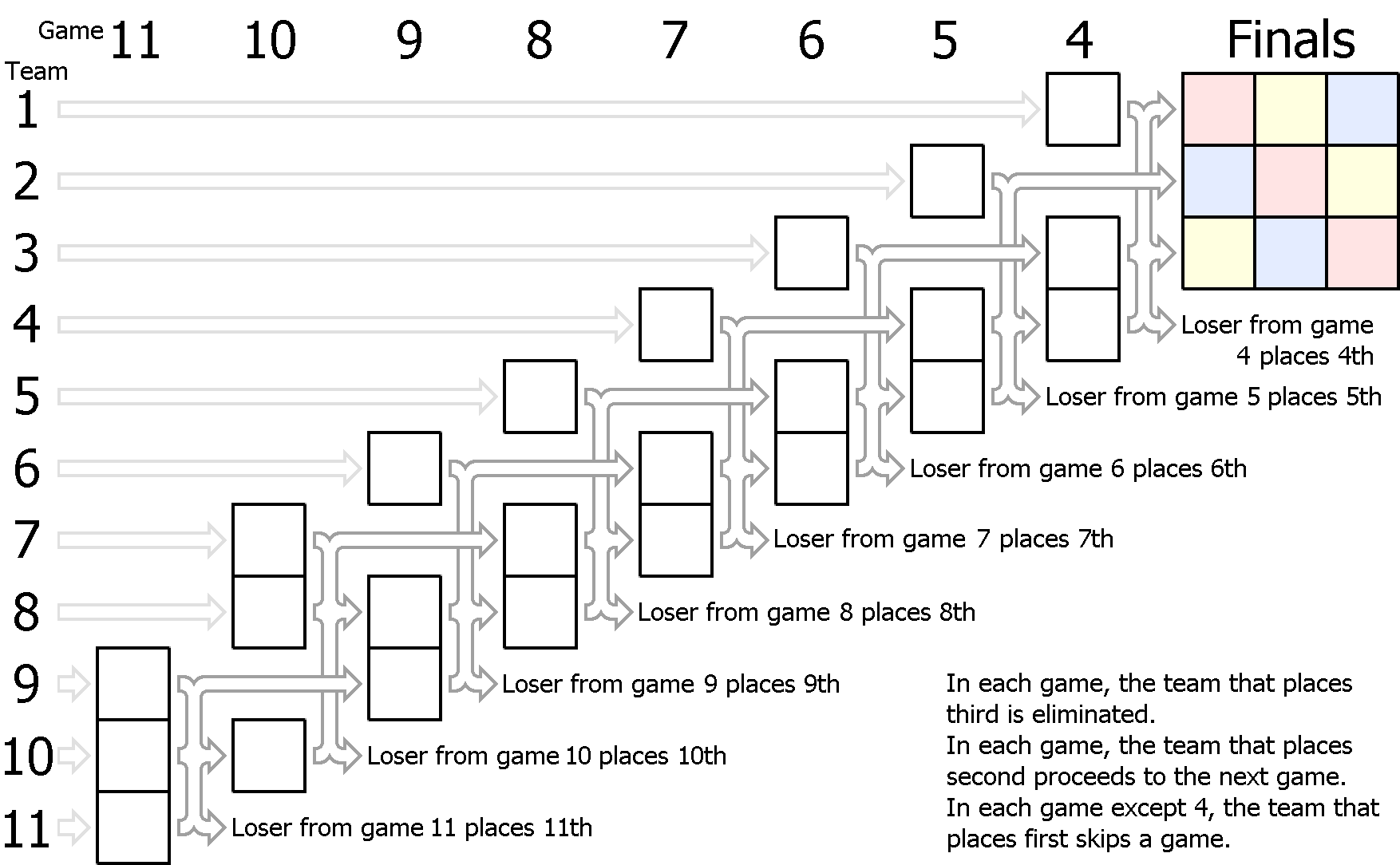
(Also diagrams for Skip Ascension regular and Skip Ascension Irregular, which have the other two possible combinations of start and end.)
Strategy: Place as high as you can.
Advanced Strategy: If there is a team you would rather not see in a future game, play so as to make them come third. (But in doing this, you must be careful not to compromise your ability to come first.)
Pros:
Cons:
Below are two versions of Format D. The difference between the two is just how the games are arranged: in the first one, they are arranged to make it easy to understand how it conceptually works; in the second, they are arranged to avoid back-to-back games (except between the first and second games).
For n teams, Format D requires (n - 1) * 1.5 games, including finals. That's just under 1.5 games per team. The average team will play 4 or 5 games.
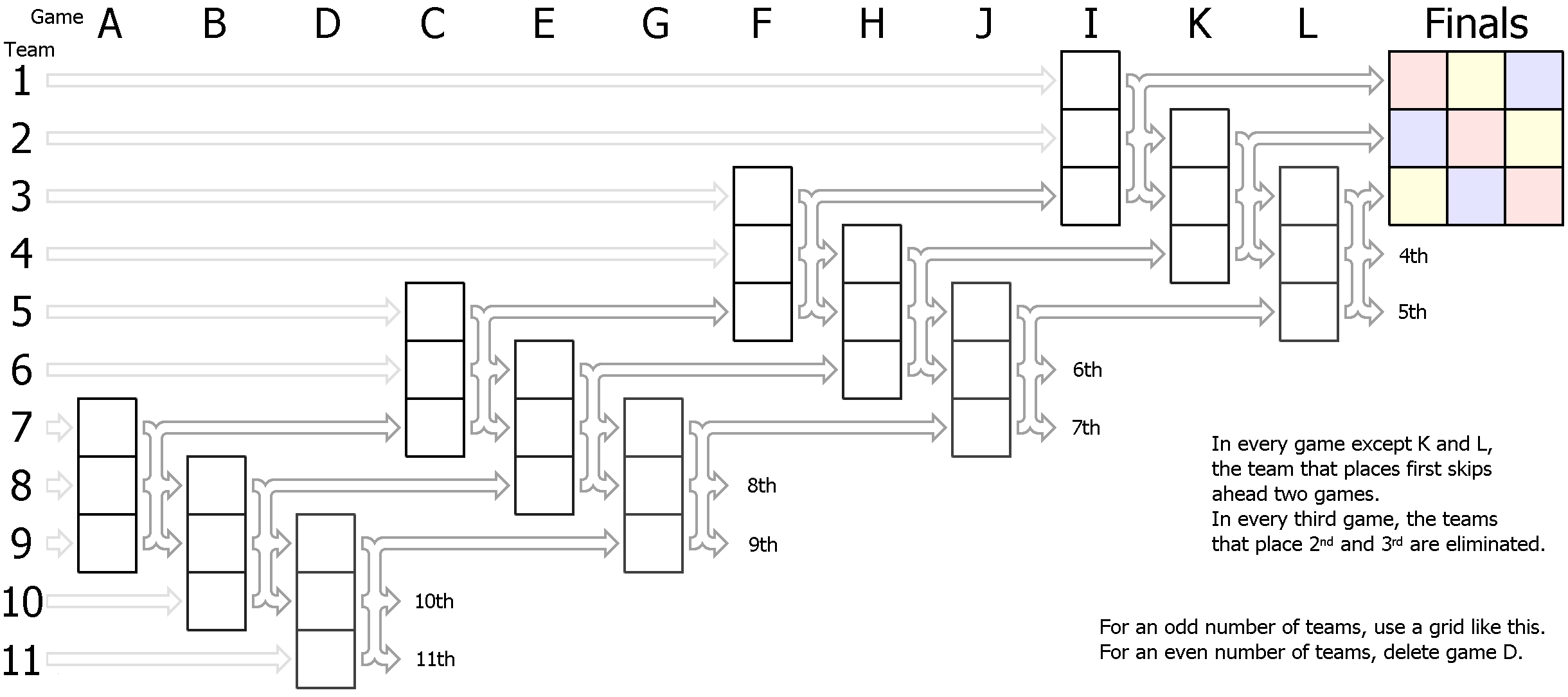

(Also diagrams for 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 33 teams; Excel workbook.)
Format D can be seen as having three roads: high, middle and low. Your first game will be on the high road. As long as you continue to take firsts, you will remain on the high road. When you lose a game, you will drop to the middle road. There is no way up from the middle to the high road. When you lose a second game, you will be on the low road, from which there is again no way up. When you lose your third game, you are eliminated.
Strategy: Come first.
Advanced Strategy: In a high road or middle road game, you may voluntarily lose in order to hand first place to a team you would like to meet in a future game. This is risky, as every time you drop to a lower road, you are at more risk of being eliminated. However, some argue that this risk may be worth taking in the last high-road game before finals (game I on the above diagrams), because it pushes a team of your choice into the finals.
Pros:
Cons:
For n teams, Two Track requires n + 1 games, including finals. The average team will play 3 games.
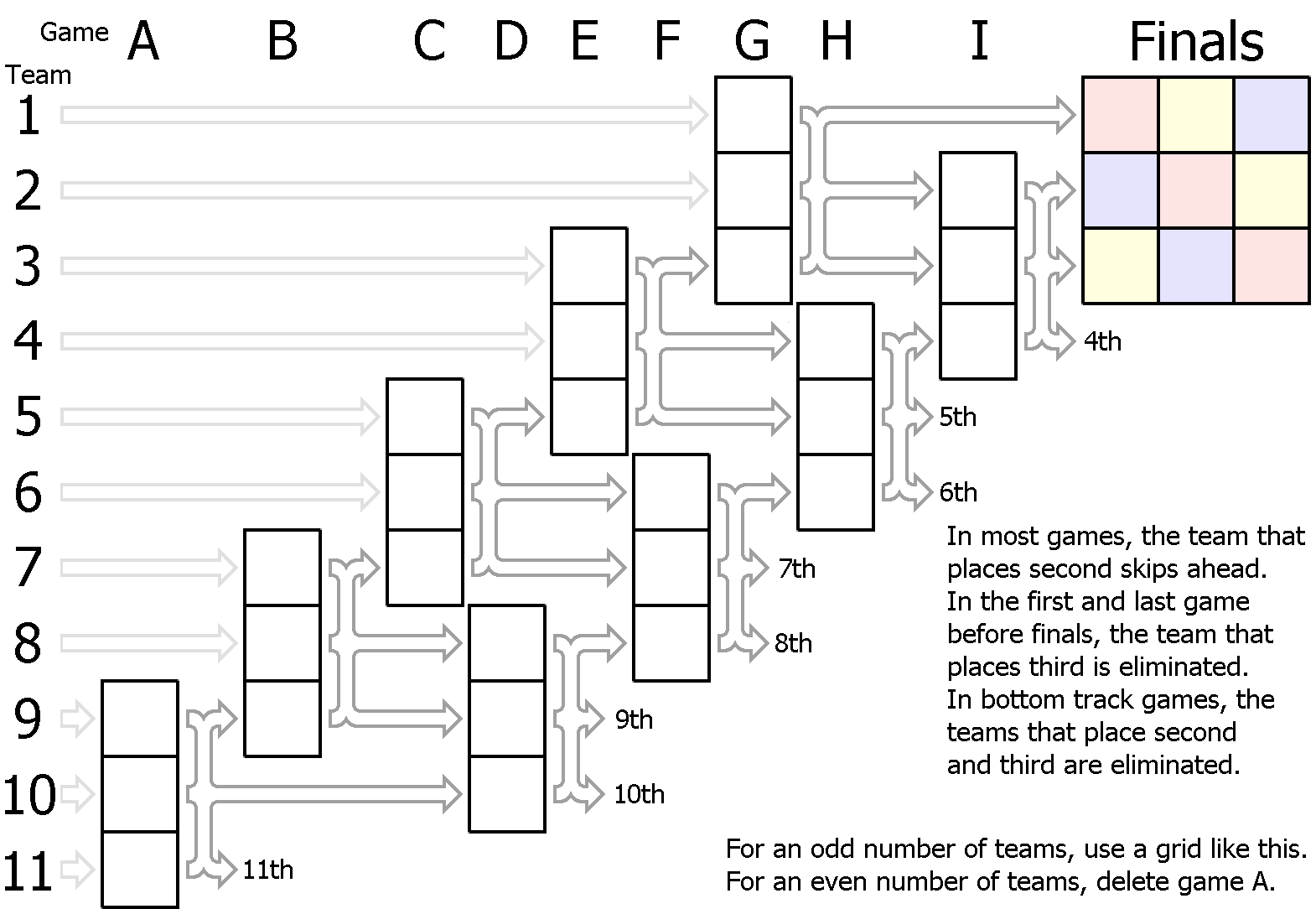
(Also diagrams for 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 19 teams.)
Two Track can be seen as being like Format D with the bottom road removed. If you keep taking firsts, you stay on the high road. Once you take a second or third, you drop to the low road. There is no way back up from the low road to the high road. Once you lose a second game, you are eliminated.
Strategy: Come first. In game I, come first or second.
Pros:
Cons:
By shade.
Just as finals is a three-game series, the last game of semifinals can be made into a two game series. Colours are chosen such that no team plays the same colour twice. Scores are summed (or averaged) over the two games. This feature can be added to any semifinals scheme, regardless of whether the top 1 or the top 2 from this game advance to finals.
Strategy: Place as well as you can.
Advanced Strategy: If two teams from this game will advance to finals, decide which team you do not wish to advance, and make them come third.
Pros:
Cons:
Four Track (which can obviously be extended to n tracks). (Our experience with a 5-track at the Aus Nats Lord of the Ring in 2013 showed that you wind up playing the same opponents over and over, and it doesn't add more fun or more accurate ranking.)
Descension, Skip Descension, Descending D, Descending D with bodge,
Two Track Descending, Two Track Descending 2, with a different connection between first and second tracks, and with bodge.
Two Track with n teams per game, Format D with n teams per game. Suppose you had 8 teams in each game, and you decide that 3 teams make the cut in each game. In these diagrams, each narrow arrow would then represent 3 teams, and each wide arrow 8 − 3 = 5 teams. Note that in the last game before finals, the cuts may be different.
Many other semifinals schemes are possible. I allege that the following properties are good:
Many of these goals contradict each other: all schemes, therefore, are compromises.
As mentioned above, in all these systems, the top team going in to each game has first choice of colour, the second team has scond choice, and the third team gets what they get.
In arenas where all three colours are approximately even, this makes little difference. But in arenas where colour matters a lot -- for example, a particular colour almost always wins, or a particular colour almost always loses, it makes a major difference, and upsets become rarer. For an example of this, see the semifinals of the New Zealand Invitational 2008, in which blue lost every game but one, and every team came out of the semifinals with the same rank they went in (though WA and VIC subsequently swapped places in the grand final).
If this is regarded as undesirable, the arena itself can be modified to be more even. Another approach would be to apply a handicap: if a particular colour always wins, multiply that colour's score by 0.9; if a particular colour always loses, multiply its score by 1.1. Keep increasing these multipliers until all colours win approximately evenly, or until teams make less consistent choices of colour in semifinals games. But such tuning should be done before semifinals day, and any multipliers should apply through the whole tournament, not just in semifinals games, in order that teams are continuing to play games that are as similar as possible to the games they've been practising through the main part of the tournament.